Header file for gensvm_update.c. More...

Go to the source code of this file.
Functions | |
| double | gensvm_calculate_omega (struct GenModel *model, struct GenData *data, long i) |
| Calculate the value of omega for a single instance. More... | |
| bool | gensvm_majorize_is_simple (struct GenModel *model, struct GenData *data, long i) |
| Check if we can do simple majorization for a given instance. More... | |
| void | gensvm_calculate_ab_non_simple (struct GenModel *model, long i, long j, double *a, double *b_aq) |
| Compute majorization coefficients for non-simple instance. More... | |
| void | gensvm_calculate_ab_simple (struct GenModel *model, long i, long j, double *a, double *b_aq) |
| Compute majorization coefficients for simple instances. More... | |
| double | gensvm_get_alpha_beta (struct GenModel *model, struct GenData *data, long i, double *beta) |
| Compute the alpha_i and beta_i for an instance. More... | |
| void | gensvm_get_update (struct GenModel *model, struct GenData *data, struct GenWork *work) |
| Perform a single step of the majorization algorithm to update V. More... | |
| void | gensvm_get_ZAZ_ZB_dense (struct GenModel *model, struct GenData *data, struct GenWork *work) |
| Calculate Z'*A*Z and Z'*B for dense matrices. More... | |
| void | gensvm_get_ZAZ_ZB_sparse (struct GenModel *model, struct GenData *data, struct GenWork *work) |
| Calculate Z'*A*Z and Z'*B for sparse matrices. More... | |
| void | gensvm_get_ZAZ_ZB (struct GenModel *model, struct GenData *data, struct GenWork *work) |
| Wrapper around calculation of Z'*A*Z and Z'*B for sparse and dense. More... | |
| int | dposv (char UPLO, int N, int NRHS, double *A, int LDA, double *B, int LDB) |
| Solve AX = B where A is symmetric positive definite. More... | |
| int | dsysv (char UPLO, int N, int NRHS, double *A, int LDA, int *IPIV, double *B, int LDB, double *WORK, int LWORK) |
| Solve a system of equations AX = B where A is symmetric. More... | |
Detailed Description
Header file for gensvm_update.c.
- Date
- 2016-10-14
- Copyright
- Copyright 2016, G.J.J. van den Burg.
This file is part of GenSVM.
GenSVM is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.
GenSVM is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
You should have received a copy of the GNU General Public License along with GenSVM. If not, see http://www.gnu.org/licenses/.
Definition in file gensvm_update.h.
Function Documentation
◆ dposv()
| int dposv | ( | char | UPLO, |
| int | N, | ||
| int | NRHS, | ||
| double * | A, | ||
| int | LDA, | ||
| double * | B, | ||
| int | LDB | ||
| ) |
Solve AX = B where A is symmetric positive definite.
Solve a linear system of equations AX = B where A is symmetric positive definite. This function is a wrapper for the external LAPACK routine dposv.
- Parameters
-
[in] UPLO which triangle of A is stored [in] N order of A [in] NRHS number of columns of B [in,out] A double precision array of size (LDA, N). On exit contains the upper or lower factor of the Cholesky factorization of A. [in] LDA leading dimension of A [in,out] B double precision array of size (LDB, NRHS). On exit contains the N-by-NRHS solution matrix X. [in] LDB the leading dimension of B
- Returns
- info parameter which contains the status of the computation:
- =0: success
- <0: if -i, the i-th argument had an illegal value
- >0: if i, the leading minor of A was not positive definite
See the LAPACK documentation at: http://www.netlib.org/lapack/explore-html/dc/de9/group__double_p_osolve.html
Definition at line 592 of file gensvm_update.c.
◆ dsysv()
| int dsysv | ( | char | UPLO, |
| int | N, | ||
| int | NRHS, | ||
| double * | A, | ||
| int | LDA, | ||
| int * | IPIV, | ||
| double * | B, | ||
| int | LDB, | ||
| double * | WORK, | ||
| int | LWORK | ||
| ) |
Solve a system of equations AX = B where A is symmetric.
Solve a linear system of equations AX = B where A is symmetric. This function is a wrapper for the external LAPACK routine dsysv.
- Parameters
-
[in] UPLO which triangle of A is stored [in] N order of A [in] NRHS number of columns of B [in,out] A double precision array of size (LDA, N). On exit contains the block diagonal matrix D and the multipliers used to obtain the factor U or L from the factorization A = U*D*U**T or A = L*D*L**T. [in] LDA leading dimension of A [in] IPIV integer array containing the details of D [in,out] B double precision array of size (LDB, NRHS). On exit contains the N-by-NRHS matrix X [in] LDB leading dimension of B [out] WORK double precision array of size max(1,LWORK). On exit, WORK(1) contains the optimal LWORK [in] LWORK the length of WORK, can be used for determining the optimal blocksize for dsystrf.
- Returns
- info parameter which contains the status of the computation:
- =0: success
- <0: if -i, the i-th argument had an illegal value
- >0: if i, D(i, i) is exactly zero, no solution can be computed.
See the LAPACK documentation at: http://www.netlib.org/lapack/explore-html/d6/d0e/group__double_s_ysolve.html
Definition at line 637 of file gensvm_update.c.
◆ gensvm_calculate_ab_non_simple()
| void gensvm_calculate_ab_non_simple | ( | struct GenModel * | model, |
| long | i, | ||
| long | j, | ||
| double * | a, | ||
| double * | b_aq | ||
| ) |
Compute majorization coefficients for non-simple instance.
In this function we compute the majorization coefficients needed for an instance with a non-simple majorization ( 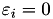 ). In this function, we distinguish a number of cases depending on the value of GenModel::p and the respective value of
). In this function, we distinguish a number of cases depending on the value of GenModel::p and the respective value of 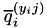 . Note that the linear coefficient is of the form
. Note that the linear coefficient is of the form 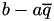 , but often the second term is included in the definition of
, but often the second term is included in the definition of 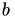 , so it can be optimized out. The output argument
, so it can be optimized out. The output argument b_aq contains this difference therefore in one go. More details on this function can be found in the Implementation details for majorization steps. See also gensvm_calculate_ab_simple().
- Parameters
-
[in] model GenModel structure with the current model [in] i index for the instance [in] j index for the class [out] *a output argument for the quadratic coefficient [out] *b_aq output argument for the linear coefficient.
Definition at line 126 of file gensvm_update.c.
◆ gensvm_calculate_ab_simple()
| void gensvm_calculate_ab_simple | ( | struct GenModel * | model, |
| long | i, | ||
| long | j, | ||
| double * | a, | ||
| double * | b_aq | ||
| ) |
Compute majorization coefficients for simple instances.
In this function we compute the majorization coefficients needed for an instance with a simple majorization. This corresponds to the non-simple majorization for the case where GenModel::p equals 1. Due to this condition the majorization coefficients are quite simple to compute. Note that the linear coefficient of the majorization is of the form 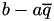 , but often the second term is included in the definition of
, but often the second term is included in the definition of 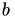 , so it can be optimized out. For more details see the Implementation details for majorization steps, and gensvm_calculate_ab_non_simple().
, so it can be optimized out. For more details see the Implementation details for majorization steps, and gensvm_calculate_ab_non_simple().
- Parameters
-
[in] model GenModel structure with the current model [in] i index for the instance [in] j index for the class [out] *a output argument for the quadratic coefficient [out] *b_aq output argument for the linear coefficient
Definition at line 183 of file gensvm_update.c.
◆ gensvm_calculate_omega()
Calculate the value of omega for a single instance.
This function calculates the value of the 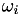 variable for a single instance, where
variable for a single instance, where
![\[ \omega_i = \frac{1}{p} \left( \sum_{j \neq y_i} h^p\left( \overline{q}_i^{(y_i j)} \right) \right)^{1/p-1} \]](form_67.png)
Note that his function uses the precalculated values from GenModel::H and GenModel::R to speed up the computation.
- Parameters
-
[in] model GenModel structure with the current model [in] data GenData structure with the data (used for y) [in] i index of the instance for which to calculate omega
- Returns
- the value of omega for instance i
Definition at line 56 of file gensvm_update.c.
◆ gensvm_get_alpha_beta()
| double gensvm_get_alpha_beta | ( | struct GenModel * | model, |
| struct GenData * | data, | ||
| long | i, | ||
| double * | beta | ||
| ) |
Compute the alpha_i and beta_i for an instance.
This computes the 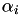 value for an instance, and simultaneously updating the row of the B matrix corresponding to that instance (the
value for an instance, and simultaneously updating the row of the B matrix corresponding to that instance (the 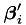 ). The advantage of doing this at the same time is that we can compute the a and b values simultaneously in the gensvm_calculate_ab_simple() and gensvm_calculate_ab_non_simple() functions.
). The advantage of doing this at the same time is that we can compute the a and b values simultaneously in the gensvm_calculate_ab_simple() and gensvm_calculate_ab_non_simple() functions.
The computation is done by first checking whether simple majorization is possible for this instance. If so, the 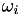 value is set to 1.0, otherwise this value is computed. If simple majorization is possible, the coefficients a and b_aq are computed by gensvm_calculate_ab_simple(), otherwise they're computed by gensvm_calculate_ab_non_simple(). Next, the beta_i updated through the efficient BLAS daxpy function, and part of the value of
value is set to 1.0, otherwise this value is computed. If simple majorization is possible, the coefficients a and b_aq are computed by gensvm_calculate_ab_simple(), otherwise they're computed by gensvm_calculate_ab_non_simple(). Next, the beta_i updated through the efficient BLAS daxpy function, and part of the value of 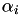 is computed. The final value of
is computed. The final value of 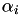 is returned.
is returned.
- Parameters
-
[in] model GenModel structure with the current model [in] data GenData structure with the data [in] i index of the instance to update [out] beta beta vector of linear coefficients (assumed to be allocated elsewhere, initialized here)
- Returns
- the
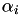 value of this instance
value of this instance
Definition at line 228 of file gensvm_update.c.
◆ gensvm_get_update()
Perform a single step of the majorization algorithm to update V.
This function contains the main update calculations of the algorithm. These calculations are necessary to find a new update V. The calculations exist of recalculating the majorization coefficients for all instances and all classes, and solving a linear system to find V.
Because the function gensvm_get_update() is always called after a call to gensvm_get_loss() with the same GenModel::V, it is unnecessary to calculate the updated errors GenModel::Q and GenModel::H here too. This saves on computation time.
In calculating the majorization coefficients we calculate the elements of a diagonal matrix A with elements
![\[ A_{i, i} = \frac{1}{n} \rho_i \sum_{j \neq k} \left[ \varepsilon_i a_{ijk}^{(1)} + (1 - \varepsilon_i) \omega_i a_{ijk}^{(p)} \right], \]](form_72.png)
where 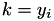 . Since this matrix is only used to calculate the matrix
. Since this matrix is only used to calculate the matrix 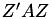 , it is efficient to update a matrix ZAZ through consecutive rank 1 updates with a single element of A and the corresponding row of Z. The BLAS function dsyr is used for this.
, it is efficient to update a matrix ZAZ through consecutive rank 1 updates with a single element of A and the corresponding row of Z. The BLAS function dsyr is used for this.
The B matrix is has rows
![\[ \boldsymbol{\beta}_i' = \frac{1}{n} \rho_i \sum_{j \neq k} \left[ \varepsilon_i \left( b_{ijk}^{(1)} - a_{ijk}^{(1)} \overline{q}_i^{(kj)} \right) + (1 - \varepsilon_i) \omega_i \left( b_{ijk}^{(p)} - a_{ijk}^{(p)} \overline{q}_i^{(kj)} \right) \right] \boldsymbol{\delta}_{kj}' \]](form_75.png)
This is also split into two cases, one for which 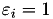 , and one for when it is 0. The 3D simplex difference matrix is used here, in the form of the
, and one for when it is 0. The 3D simplex difference matrix is used here, in the form of the 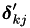 .
.
Finally, the following system is solved
![\[ (\textbf{Z}'\textbf{AZ} + \lambda \textbf{J})\textbf{V} = (\textbf{Z}'\textbf{AZ}\overline{\textbf{V}} + \textbf{Z}' \textbf{B}) \]](form_78.png)
solving this system is done through dposv().
- Todo:
- Consider using CblasColMajor everywhere
- Parameters
-
[in,out] model model to be updated [in] data data used in model [in] work allocated workspace to use
Definition at line 323 of file gensvm_update.c.
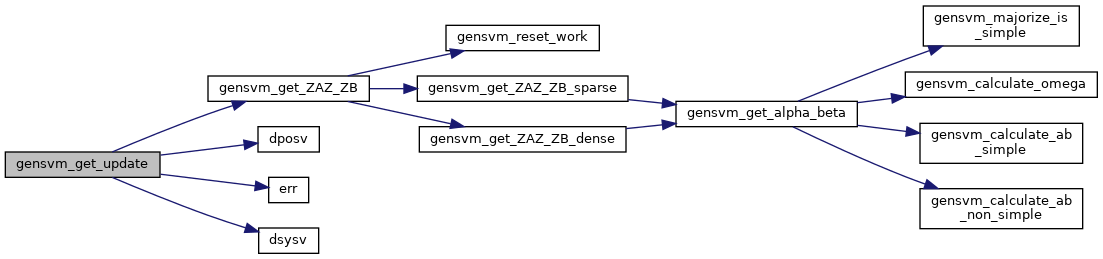
◆ gensvm_get_ZAZ_ZB()
Wrapper around calculation of Z'*A*Z and Z'*B for sparse and dense.
This is a wrapper around gensvm_get_ZAZ_ZB_dense() and gensvm_get_ZAZ_ZB_sparse(). See the documentation of those functions for more info.
Definition at line 552 of file gensvm_update.c.
◆ gensvm_get_ZAZ_ZB_dense()
| void gensvm_get_ZAZ_ZB_dense | ( | struct GenModel * | model, |
| struct GenData * | data, | ||
| struct GenWork * | work | ||
| ) |
Calculate Z'*A*Z and Z'*B for dense matrices.
This function calculates the matrices Z'A*Z and Z'*B for the case where Z is stored as a dense matrix. It calculates the Z'*A*Z product by constructing a matrix LZ = (A^(1/2) * Z), and calculating (LZ)'(LZ) with the BLAS dsyrk function. The matrix Z'*B is calculated with successive rank-1 updates using the BLAS dger function. These functions came out as the most efficient way to do these computations in several simulation studies.
- Parameters
-
[in] model a GenModel holding the current model [in] data a GenData with the data [in,out] work an allocated GenWork structure, contains updated ZAZ and ZB matrices on exit.
Definition at line 418 of file gensvm_update.c.
◆ gensvm_get_ZAZ_ZB_sparse()
| void gensvm_get_ZAZ_ZB_sparse | ( | struct GenModel * | model, |
| struct GenData * | data, | ||
| struct GenWork * | work | ||
| ) |
Calculate Z'*A*Z and Z'*B for sparse matrices.
This function calculates the matrices Z'*A*Z and Z'*B for the case where Z is stored as a CSR sparse matrix (GenSparse structure). It computes only the products of the Z'*A*Z matrix that need to be computed, and updates the Z'*B matrix row-wise for each non-zero element of a row of Z, using a BLAS daxpy call.
This function calculates the matrix product Z'*A*Z in separate blocks, based on the number of rows defined in the GENSVM_BLOCK_SIZE variable. This is done to improve numerical precision for very large datasets. Due to rounding errors, precision can become an issue for these large datasets, when separate blocks are used and added to the result separately, this can be alleviated a little bit. See also: http://stackoverflow.com/q/40286989
- Parameters
-
[in] model a GenModel holding the current model [in] data a GenData with the data [in,out] work an allocated GenWork structure, contains updated ZAZ and ZB matrices on exit.
Definition at line 481 of file gensvm_update.c.
◆ gensvm_majorize_is_simple()
Check if we can do simple majorization for a given instance.
A simple majorization is possible if at most one of the Huberized hinge errors is nonzero for an instance. This is checked here. For this we compute the product of the Huberized error for all  and check if strictly less than 2 are nonzero. See also the Implementation details for majorization steps.
and check if strictly less than 2 are nonzero. See also the Implementation details for majorization steps.
- Parameters
-
[in] model GenModel structure with the current model [in] data GenData structure with the data (used for y) [in] i index of the instance for which to check
- Returns
- whether or not we can do simple majorization
Definition at line 89 of file gensvm_update.c.
 1.8.13
1.8.13