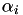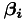This page explains the translation from the mathematics in the paper for computing the $\alpha_i$ and $\boldsymbol{\beta_i}$ values, to the implementation in the code. It is here mostly for future reference and documentation purposes, you won't actually need to understand this in order to use GenSVM.

Computation of the quadratic coefficients

We start our analysis with the computation of the 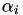$\alpha_i$ :

$\alpha_i = \frac{1}{n} \rho_i \sum_{j \neq y_i} \left[ \varepsilon_i a_{ijy_i}^{(1)} + (1 - \varepsilon_i) \omega_i a_{ijy_i}^{(p)} \right]$

Since in the code in gensvm_get_Avalue_update_B() we work with a condition on the 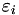$\varepsilon_i$ , we will write the 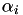$\alpha_i$ using this condition as well:

$\alpha_i = \begin{dcases} \frac{1}{n} \rho_i \sum_{j \neq y_i} a_{ijy_i}^{(1)} & \text{ if } \varepsilon_i = 1 \\ \frac{1}{n} \rho_i \omega_i \sum_{j \neq y_i} a_{ijy_i}^{(p)} & \text{ if } \varepsilon_i = 0 \end{dcases}$

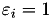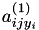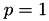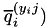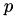Now, if $\varepsilon_i = 1$ , we need to calculate the $a_{ijy_i}^{(1)}$ , corresponding to $p = 1$ . From the overview of quadratic majorization coefficients given in the paper, we see that there are five regions for the coefficient depending on the value of $\overline{q}_i^{(y_ij})$ and $p$ . However, with 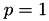$p = 1$ , this reduces to three regions, since 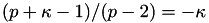$(p + \kappa - 1)/(p - 2) = -\kappa$ if $p = 1$ . 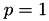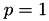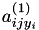Plugging in $p = 1$ in the formulas from the table yields the following expressions for $a_{ijy_i}^{(1)}$ :

$a_{ijy_i}^{(1)} = \begin{dcases} \frac{1}{4} \left( 1 - \overline{q}_i^{(y_ij)} - \frac{\kappa + 1}{2} \right)^{-1} & \text{ if } \overline{q}_i^{(y_ij)} \leq -\kappa \\ \frac{1}{2(\kappa + 1)} & \text{ if } \overline{q}_i^{(y_ij)} \in (-\kappa, 1] \\ -\frac{1}{4} \left( 1 - \overline{q}_i^{(y_ij)} - \frac{\kappa + 1}{2} \right)^{-1} & \text{ if } \overline{q}_i^{(y_ij)} > 1 \end{dcases}$

These coefficients should correspond to the coefficients for 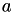$a$ as calculated in gensvm_calculate_ab_simple().

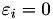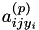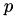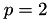If $\varepsilon_i = 0$ , we need to calculate $a_{ijy_i}^{(p)}$ . Here, we distinguish two cases depending on the value of $p$ . If $p = 2 $ , the value of 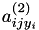$a_{ijy_i}^{(2)}$ is the same everywhere, and equal to 1.5. Otherwise, if 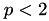$p < 2$ , we have

$a_{ijy_i}^{(p)} = \begin{dcases} \frac{1}{4} p^2 \left( 1 - \overline{q}_i^{(y_ij)} - \frac{\kappa + 1}{2} \right)^{p - 2} & \text{ if } \overline{q}_i^{(y_ij)} \leq \frac{p + \kappa - 1}{p - 2} \\ \frac{1}{4} p (2p - 1) \left( \frac{\kappa + 1}{2} \right)^{p - 2} & \text{ if } \overline{q}_i^{(y_ij)} \in \left( \left. \frac{p + \kappa - 1}{p - 2}, 1 \right. \right] \\ \frac{1}{4} p^2 \left( \frac{p}{p - 2} \left( 1 - \overline{q}_i^{(y_ij)} - \frac{\kappa + 1}{2}\right) \right)^{p - 2} & \text{ if } \overline{q}_i^{(y_ij)} > 1 \end{dcases}$

Note that in the second case the expression is independent of 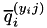$\overline{q}_i^{(y_ij)}$ , so this value can be cached. These expressions for 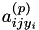$a_{ijy_i}^{(p)}$ are reflected in gensvm_calculate_ab_non_simple().

Computation of the linear coefficients

We continue the analysis with the computation of the 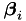$\boldsymbol{\beta}_i$ vectors. These vectors are given by the expression:

$\boldsymbol{\beta}_i' = \frac{1}{n}\rho_i \sum_{j \neq y_i} \left[ \varepsilon_i \left( b_{ijy_i}^{(1)} - a_{ijy_i}^{(1)}\overline{q}_i^{(y_ij)} \right) + (1 - \varepsilon_i) \omega_i \left( b_{ijy_i}^{(p)} - a_{ijy_i}^{(p)}\overline{q}_i^{(y_ij)} \right) \right] \boldsymbol{\delta}_{y_ij}'$

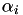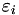Similarly to the $\alpha_i$ above, we can write this in two cases depending on $\varepsilon_i$ :

$\boldsymbol{\beta}_i' = \begin{dcases} \frac{1}{n}\rho_i \sum_{j \neq y_i} \left( b_{ijy_i}^{(1)} - a_{ijy_i}^{(1)}\overline{q}_i^{(y_ij)} \right) \boldsymbol{\delta}_{y_ij}' & \text{ if } \varepsilon_i = 1 \\ \frac{1}{n}\rho_i \omega_i \sum_{j \neq y_i} \left( b_{ijy_i}^{(p)} - a_{ijy_i}^{(p)}\overline{q}_i^{(y_ij)} \right) \boldsymbol{\delta}_{y_ij}' & \text{ if } \varepsilon_i = 0 \end{dcases}$

In the code we directly compute the differences of the form 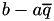$b - a\overline{q}$ , since this is saves some computations. We therefore work out the values of these expressions below.

First, for 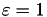$\varepsilon = 1$ we have, after plugging in 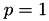$p = 1$ and rearranging:

$b_{ijy_i}^{(1)} - a_{ijy_i}^{(1)}\overline{q}_i^{(y_ij)} = \begin{dcases} \frac{1}{2} & \text{ if } \overline{q}_i^{(y_ij)} \leq -\kappa \\ a_{ijy_i}^{(1)} \left( 1 - \overline{q}_i^{(y_ij)} \right) & \text{ if } \overline{q}_i^{(y_ij)} \in (-\kappa, 1] \\ 0 & \text{ if } \overline{q}_i^{(y_ij)} > 1 \end{dcases}$

(the final 0 may be surprising, but can be found when plugging in the value of 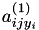$a_{ijy_i}^{(1)}$ ). The above coefficients for this difference are reflected in gensvm_calculate_ab_simple().

Now for 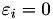$\varepsilon_i = 0$ , we first have the case where 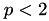$p < 2$ , then

$b_{ijy_i}^{(p)} - a_{ijy_i}^{(p)}\overline{q}_i^{(y_ij)} = \begin{dcases} \frac{1}{2}p\left( 1 - \overline{q}_i^{(y_ij)} - \frac{\kappa + 1}{2}\right)^{p-1} & \text{ if } \overline{q}_i^{(y_ij)} \leq -\kappa \\ \frac{p \left(1 - \overline{q}_i^{(y_ij)} \right)^{2p-1}}{ \left(2(\kappa + 1)\right)^p} & \text{ if } \overline{q}_i^{(y_ij)} \in (-\kappa, 1] \\ a_{ijy_i}^{(p)} \left( \frac{2\overline{q}_i^{(y_ij)} + \kappa - 1}{p - 2} \right) + \frac{1}{2} p \left( \frac{p}{p - 2} \left(1 - \overline{q}_i^{(y_ij)} - \frac{\kappa + 1}{2} \right) \right)^{p - 1} & \text{ if } \overline{q}_i^{(y_ij)} > 1 \end{dcases}$

Second, we have the case where 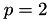$ p = 2$ , in that case:

$b_{ijy_i}^{(2)} - a_{ijy_i}^{(2)}\overline{q}_i^{(y_ij)} = \begin{dcases} 1 - \overline{q}_i^{(y_ij)} - \frac{\kappa + 1}{2} & \text{ if } \overline{q}_i^{(y_ij)} \leq -\kappa \\ \frac{1}{2(\kappa+1)^2}\left( 1 - \overline{q}_i^{(y_ij)} \right)^3 & \text{ if } \overline{q}_i^{(y_ij)} \in (-\kappa, 1] \\ 0 & \text{ if } \overline{q}_i^{(y_ij)} > 1 \end{dcases}$

These coefficients are all calculated in gensvm_calculate_ab_non_simple().