Header file for gensvm_kernel.c. More...
#include "gensvm_base.h"
Go to the source code of this file.
Functions | |
| void | gensvm_kernel_copy_kernelparam_to_data (struct GenModel *model, struct GenData *data) |
| Copy the kernelparameters from GenModel to GenData. More... | |
| void | gensvm_kernel_preprocess (struct GenModel *model, struct GenData *data) |
| Do the preprocessing steps needed to perform kernel GenSVM. More... | |
| void | gensvm_kernel_postprocess (struct GenModel *model, struct GenData *traindata, struct GenData *testdata) |
| Compute the kernel postprocessing factor. More... | |
| void | gensvm_kernel_compute (struct GenModel *model, struct GenData *data, double *K) |
| Compute the kernel matrix. More... | |
| long | gensvm_kernel_eigendecomp (double *K, long n, double cutoff, double **P_ret, double **Sigma_ret) |
| Find the (reduced) eigendecomposition of a kernel matrix. More... | |
| double * | gensvm_kernel_cross (struct GenModel *model, struct GenData *data_train, struct GenData *data_test) |
| Compute the kernel crossproduct between two datasets. More... | |
| void | gensvm_kernel_trainfactor (struct GenData *data, double *P, double *Sigma, long r) |
| Compute the training factor as part of kernel preprocessing. More... | |
| void | gensvm_kernel_testfactor (struct GenData *testdata, struct GenData *traindata, double *K2) |
| Calculate the matrix product for the testfactor. More... | |
| double | gensvm_kernel_dot_rbf (double *x1, double *x2, long n, double gamma) |
| Compute the RBF kernel between two vectors. More... | |
| double | gensvm_kernel_dot_poly (double *x1, double *x2, long n, double gamma, double coef, double degree) |
| Compute the polynomial kernel between two vectors. More... | |
| double | gensvm_kernel_dot_sigmoid (double *x1, double *x2, long n, double gamma, double coef) |
| Compute the sigmoid kernel between two vectors. More... | |
| int | dsyevx (char JOBZ, char RANGE, char UPLO, int N, double *A, int LDA, double VL, double VU, int IL, int IU, double ABSTOL, int *M, double *W, double *Z, int LDZ, double *WORK, int LWORK, int *IWORK, int *IFAIL) |
| Compute the eigenvalues and optionally the eigenvectors of a symmetric matrix. More... | |
| double | dlamch (char CMACH) |
| Determine double precision machine parameters. More... | |
Detailed Description
Header file for gensvm_kernel.c.
- Date
- 2014-01-07
Contains function declarations for computing the kernel matrix in nonlinear MSVMGen. Additional kernel functions should be included here and in gensvm_kernel.c
- Copyright
- Copyright 2016, G.J.J. van den Burg.
This file is part of GenSVM.
GenSVM is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.
GenSVM is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
You should have received a copy of the GNU General Public License along with GenSVM. If not, see http://www.gnu.org/licenses/.
Definition in file gensvm_kernel.h.
Function Documentation
◆ dlamch()
| double dlamch | ( | char | CMACH | ) |
Determine double precision machine parameters.
This is a wrapper function around the external LAPACK function.
See the LAPACK documentation at: http://www.netlib.org/lapack/explore-html/d5/dd4/dlamch_8f.html
Definition at line 575 of file gensvm_kernel.c.
◆ dsyevx()
| int dsyevx | ( | char | JOBZ, |
| char | RANGE, | ||
| char | UPLO, | ||
| int | N, | ||
| double * | A, | ||
| int | LDA, | ||
| double | VL, | ||
| double | VU, | ||
| int | IL, | ||
| int | IU, | ||
| double | ABSTOL, | ||
| int * | M, | ||
| double * | W, | ||
| double * | Z, | ||
| int | LDZ, | ||
| double * | WORK, | ||
| int | LWORK, | ||
| int * | IWORK, | ||
| int * | IFAIL | ||
| ) |
Compute the eigenvalues and optionally the eigenvectors of a symmetric matrix.
This is a wrapper function around the external LAPACK function.
See the LAPACK documentation at: http://www.netlib.org/lapack/explore-html/d2/d97/dsyevx_8f.html
Definition at line 550 of file gensvm_kernel.c.
◆ gensvm_kernel_compute()
Compute the kernel matrix.
This function computes the kernel matrix of a data matrix based on the requested kernel type and the kernel parameters. The potential types of kernel functions are document in KernelType. This function uses a naive multiplication and computes the entire upper triangle of the kernel matrix, then copies this over to the lower triangle.
- Parameters
-
[in] model a GenModel structure with the model [in] data a GenData structure with the data [out] K an nxn preallocated kernel matrix
Definition at line 157 of file gensvm_kernel.c.
◆ gensvm_kernel_copy_kernelparam_to_data()
◆ gensvm_kernel_cross()
| double* gensvm_kernel_cross | ( | struct GenModel * | model, |
| struct GenData * | data_train, | ||
| struct GenData * | data_test | ||
| ) |
Compute the kernel crossproduct between two datasets.
Given a training set 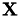 with feature space mapping
with feature space mapping 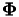 and a test set
and a test set 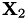 with feature space mapping
with feature space mapping 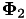 , the crosskernel
, the crosskernel 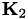 is given by
is given by 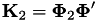 . Thus, an element in row
. Thus, an element in row 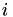 and column
and column 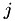 in
in 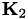 equals the kernel product between the
equals the kernel product between the 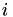 -th row of
-th row of 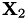 and the
and the 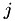 -th row of
-th row of 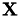 .
.
- Parameters
-
[in] model the GenSVM model [in] data_train the training dataset [in] data_test the test dataset
- Returns
- the matrix
Definition at line 311 of file gensvm_kernel.c.
◆ gensvm_kernel_dot_poly()
| double gensvm_kernel_dot_poly | ( | double * | x1, |
| double * | x2, | ||
| long | n, | ||
| double | gamma, | ||
| double | coef, | ||
| double | degree | ||
| ) |
Compute the polynomial kernel between two vectors.
The polynomial kernel is computed between two vectors. This kernel is defined as
![\[ k(x_1, x_2) = ( \gamma \langle x_1, x_2 \rangle + coef)^{degree} \]](form_79.png)
where 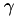 ,
, 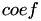 and
and 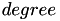 are kernel parameters.
are kernel parameters.
- Parameters
-
[in] x1 first vector [in] x2 second vector [in] n length of the vectors x1 and x2 [in] gamma gamma parameter of the kernel [in] coef coef parameter of the kernel [in] degree degree parameter of the kernel
- Returns
- kernel evaluation
Definition at line 503 of file gensvm_kernel.c.
◆ gensvm_kernel_dot_rbf()
| double gensvm_kernel_dot_rbf | ( | double * | x1, |
| double * | x2, | ||
| long | n, | ||
| double | gamma | ||
| ) |
Compute the RBF kernel between two vectors.
The RBF kernel is computed between two vectors. This kernel is defined as
![\[ k(x_1, x_2) = \exp( -\gamma \| x_1 - x_2 \|^2 ) \]](form_55.png)
where 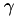 is a kernel parameter specified.
is a kernel parameter specified.
- Parameters
-
[in] x1 first vector [in] x2 second vector [in] n length of the vectors x1 and x2 [in] gamma gamma parameter of the kernel
- Returns
- kernel evaluation
Definition at line 472 of file gensvm_kernel.c.
◆ gensvm_kernel_dot_sigmoid()
| double gensvm_kernel_dot_sigmoid | ( | double * | x1, |
| double * | x2, | ||
| long | n, | ||
| double | gamma, | ||
| double | coef | ||
| ) |
Compute the sigmoid kernel between two vectors.
The sigmoid kernel is computed between two vectors. This kernel is defined as
![\[ k(x_1, x_2) = \tanh( \gamma \langle x_1 , x_2 \rangle + coef) \]](form_82.png)
where 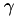 and
and 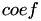 are kernel parameters.
are kernel parameters.
- Parameters
-
[in] x1 first vector [in] x2 second vector [in] n length of the vectors x1 and x2 [in] gamma gamma parameter of the kernel [in] coef coef parameter of the kernel
- Returns
- kernel evaluation
Definition at line 530 of file gensvm_kernel.c.
◆ gensvm_kernel_eigendecomp()
| long gensvm_kernel_eigendecomp | ( | double * | K, |
| long | n, | ||
| double | cutoff, | ||
| double ** | P_ret, | ||
| double ** | Sigma_ret | ||
| ) |
Find the (reduced) eigendecomposition of a kernel matrix.
Compute the reduced eigendecomposition of the kernel matrix. This uses the LAPACK function dsyevx to do the computation. Only those eigenvalues/eigenvectors are kept for which the ratio between the eigenvalue and the largest eigenvalue is larger than cutoff. This function uses the highest precision eigenvalues, twice the underflow threshold (see dsyevx documentation).
- Parameters
-
[in] K the kernel matrix [in] n the dimension of the kernel matrix [in] cutoff mimimum ratio of eigenvalue to largest eigenvalue for the eigenvector to be included [out] P_ret on exit contains the eigenvectors [out] Sigma_ret on exit contains the eigenvalues
- Returns
- the number of eigenvalues kept
Definition at line 215 of file gensvm_kernel.c.
◆ gensvm_kernel_postprocess()
| void gensvm_kernel_postprocess | ( | struct GenModel * | model, |
| struct GenData * | traindata, | ||
| struct GenData * | testdata | ||
| ) |
Compute the kernel postprocessing factor.
This function computes the postprocessing factor needed to do predictions with kernels in GenSVM. This is a wrapper around gensvm_kernel_cross() and gensvm_kernel_testfactor().
- Parameters
-
[in] model a GenSVM model [in] traindata the training dataset [in,out] testdata the test dataset. On exit, GenData::Z contains the testfactor
Definition at line 125 of file gensvm_kernel.c.
◆ gensvm_kernel_preprocess()
Do the preprocessing steps needed to perform kernel GenSVM.
To achieve nonlinearity through kernels in GenSVM, a preprocessing step is needed. This preprocessing step computes the full kernel matrix, and an eigendecomposition of this matrix. Next, it computes a matrix 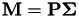 which takes the role as data matrix in the optimization algorithm.
which takes the role as data matrix in the optimization algorithm.
- See also
- gensvm_kernel_compute(), gensvm_kernel_eigendecomp(), gensvm_kernel_trainfactor(), gensvm_kernel_postprocess()
- Parameters
-
[in] model input GenSVM model [in,out] data input structure with the data. On exit, contains the training factor in GenData::Z, and the original data in GenData::RAW
Definition at line 75 of file gensvm_kernel.c.
◆ gensvm_kernel_testfactor()
| void gensvm_kernel_testfactor | ( | struct GenData * | testdata, |
| struct GenData * | traindata, | ||
| double * | K2 | ||
| ) |
Calculate the matrix product for the testfactor.
To predict class labels when kernels are used, a transformation of the testdata has to be performed to get the simplex space vectors. This transformation is based on the matrix 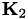 (as calculated by gensvm_make_crosskernel()) and the matrices
(as calculated by gensvm_make_crosskernel()) and the matrices 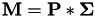 ) and
) and 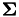 . The testfactor is equal to
. The testfactor is equal to 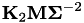 .
.
- Parameters
-
[out] testdata a GenData struct with the testdata, contains the testfactor in GenData::Z on exit preceded by a column of ones. [in] traindata a GenData struct with the training data [in] K2 crosskernel between the train and test data
Definition at line 406 of file gensvm_kernel.c.
◆ gensvm_kernel_trainfactor()
| void gensvm_kernel_trainfactor | ( | struct GenData * | data, |
| double * | P, | ||
| double * | Sigma, | ||
| long | r | ||
| ) |
Compute the training factor as part of kernel preprocessing.
This function computes the matrix product 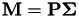 and stores the result in GenData::Z, preceded by a column of ones. It also sets GenData::r to the number of eigenvectors that were includedin P and Sigma. Note that P and Sigma correspond to the reduced eigendecomposition of the kernel matrix.
and stores the result in GenData::Z, preceded by a column of ones. It also sets GenData::r to the number of eigenvectors that were includedin P and Sigma. Note that P and Sigma correspond to the reduced eigendecomposition of the kernel matrix.
- Parameters
-
[in,out] data a GenData structure. On exit, GenData::Z and GenData::r are updated as described above. [in] P the eigenvectors [in] Sigma the eigenvalues [in] r the number of eigenvalues and eigenvectors
Definition at line 365 of file gensvm_kernel.c.
 1.8.13
1.8.13